开口运动规律
在开口过程中,经纱由综框带动作升降运动形成梭口,综框运动的性质对经纱的断头有着很大的影响。在梭口的形状和尺寸确定后,综框运动规律就成为影响开口运动效果的根本因素,对保证织造顺利进行和提高织机生产率及织物质量有着重要意义。
一、综框运动角及其分配
(一)综框运动角的表示
织机主轴每一回转,经纱形成一次梭口,其所需要的时间,称为一个开口周期。在一个开口周期内,经纱的运动经历三个时期:
1.开口时期经纱离开综平位置,上下分开,直到梭口满开为止;
2.静止时期梭口满开后,为使纬纱有足够的时间通过梭口,经纱要有一段时间静止不动;
3.闭合时期经纱经一段时间的静止后,再从梭口满开的位置返回到综平位置。
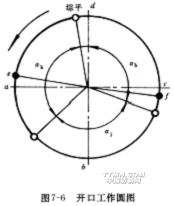
经纱从离开综平位置,上下分开,到重新返回这个位置就完成一次开口。在开口过程中,上下交替的经纱达到综平位置的时刻,即梭口开启的瞬间,称为开口时间,俗称综平时间,它是重要的工艺参数。通常,标注有织机主要机构运动时间参数的主轴圆周图称为织机工作圆图,用以表示织机运动时间的配合关系,如图7-6所示。图中箭头表示主轴回转的方向,除个别情况外,主轴总是按逆时针方向回转。圆周图的前方、下方、后方和上方四个特征位置(记为a、b、c、d)分别称为前心、下心、后心和上心。摆动筘座到达最前和最后位置e、f时,主轴所在的位置分别称为前止点(前死心)和后止点(后死心)。前止点的主轴位置角为0°,作为度量基准。图中开口时间的长短用开口角αk表示,静止时间的长短用静止角αj表示,闭口时期的长短用闭口角αb表示。在闭合和开口时期内,综框处于运动状态之中,所以αb+αk便是综框运动角。应该指出,织机主要机构运动时间的配合关系有时也用周期图表示。
(二)综框运动角的分配
开口角
二、综框运动规律
综框运动规律表示综框在运动(闭口、开口)过程中的位移与主轴转角ωt之间的关系,它对经纱断头和织机振动都有较大的影响。常见的综框运动规律有简谐运动规律和椭圆比运动规律。随着织机速度的提高,多项式运动规律也得到了较多的采用。
1.简谐运动规律
一个动点在圆周上绕圆心作等角速度运动时,此点在直径上的投影点的运动即为简谐运动。取综框在最低处(或最高处)位移s为0,综框开始闭合时主轴转角ωt为0,并设αk=αb,则综框作简谐运动的位移方程:
![]() (7-5)
(7-5)
式中:sx——任一页综框动程;
ω——织机主轴角速度;
ωt——织机主轴回转角;
αy——综框运动角,&#
对上式求导一次和二次,可得出综框运动速度v和加速度a(式子从略)。现设αy=αk+αb=(120°+120°)×π/180°=4.19rad,sx=110mm,ω=200×π/30=20.94rad/s。由此可作出综框位移s、速度v、加速度a的曲线,如图7-7中曲线A所示。
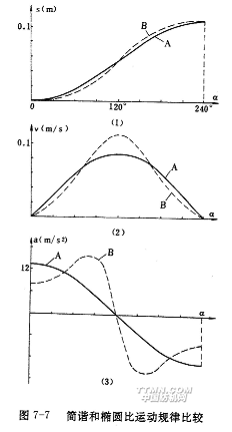
由图可见,在综平前后,综框运动迅速,此时经纱张力小,非但不会造成断头,而且有利于开清梭口;而在闭口开始后的一个时期,综框运动缓慢,对梭子飞出梭口有利。但由于综框从静止到运动和从运动到静止之间过渡时的加速度值不为零,使综框产生振动,不利于作高速运动。因此,简谐运动规律一般用于低速织机(如有梭织机)的开口机构。
2.椭圆比运动规律
一个动点在椭圆上绕中心作等角速度转动时,此点在椭圆短轴上的投影点的运动即为椭圆比运动规律。当椭圆的长、短半轴之比为1时,即为简谐运动规律。椭圆的长、短半轴之比的大小对综框运动加速度变化幅度影响很大,一般此比值取1.2~1.3。若sx、ω和αy取值同前,上述比值为1.2008时,综框加速度最大值与简谐运动规律相同,但综框从静止到运动和从运动到静止之间过渡时的加速度值比简谐运动规律小;比值大于1.2008时,综框加速度最大值超过简谐运动规律,而综框从静止到运动和从运动到静止之间过渡时的加速度值变得更小。图7-7中曲线B分别是椭圆比运动规律的位移、速度、加速度的曲线,与简谐运动规律相比,在综平前后经纱张力小时,椭圆比运动规律的综框运动速度更快,更有利于开清梭口;在闭口开始后的一个时期,综框运动更缓慢,更有利于梭子飞出梭口;综框从静止到运动和从运动到静止之间过渡时的
3.多项式运动规律
综框的多项式运动规律有多种,其中一种的位移方程为:
S=(SX/2)[35(ωt/αy)4-84(ωt/αy)5+70(ωt/αy)6-20(ωt/αy)7](7-6)
该运动规律可使综框运动开始和运动结束的瞬时加速度都为零,从而避免综框产生振动,适用于织机高速运转。
 相关信息
相关信息 







 推荐企业
推荐企业 推荐企业
推荐企业
 推荐企业
推荐企业