转杯竹节纱竹节长度与粗度的探讨

王勤泰

(上海新型纺纱技术开发中心)

摘要：从转杯纺成纱机理出发，通过对转杯竹节纱形成过程中纺杯凝聚槽内纤维增量的变化分析，探讨了转杯竹节纱竹节长度和粗度的变化规律以及不同参数设置组合与竹节形态的关系。

关键词：转杯纺纱机；竹节；基纱；长度；粗度；伺服电机

转杯纺纺制竹节纱在理论上有多种方法，但实际上最成熟的已实现工业化应用的是瑞士Amsler—Iro公司GOE装置所采用的给棉伺服变速方法，即采用微机控制瞬间超喂给棉产生竹节。上海新型纺纱技术开发中心与上海新源科技公司联合研制开发成功的CNRS一1型转杯竹节纱装置也采用这种方式。在研制过程中发现，竹节和基纱的长度与设置值相差甚远，竹节的粗度有时也会随长度的不同设置而有所差异。这一现象曾使我们怀疑是装置的哪一部分出了问题，但经研究发现是转杯竹节纱的竹节长度和粗度变化规律所致，以下就此作一浅述。

1转杯竹节纱成纱过程分析

纺制竹节纱时，由于转杯转速没有变化，转杯凝聚槽内铺设的纤维层数不变，细纱截面内纤维数的增加是靠给棉伺服电机的增速，以加大给棉量增加每层纤维束内的纤维量来实现的。给棉伺服瞬间加速后，虽使给棉输出达到纺制竹节所需的纤维量，但由于输入的新增量纤维束还是要逐层叠加铺设，并在转杯全周长内排列分布，故纱线的增粗是在转杯全周长范围内同时发生。由于纺纱是个连续的动态过程，在新增量纤维输入使细纱增粗的同时，成纱亦在不断地引出，故在从基纱一竹节转换的初始阶段，被剥离纤维层内累积的增量纤维十分有限，纱截面内纤维数量增加不多，竹节效果不明显。随着纺纱过程的延续，随后不断被剥离的纤维层内累积的增量纤维数逐渐增多，竹节也逐渐变粗，直至基纱一竹节转换过程的结束，才连续纺出所设置粗度的竹节。由于转杯内原纺基纱时滞留的相对低量纤维

层的存在，故要实现从基纱一竹节全部纤维量堆积的转换，必须待它们全部被剥离后才能完成，即经过一个转杯周长周期才能实现从基纱一竹节的彻底转换。同理，从竹节一基纱的转换过程正好相反。无论是基纱一竹节还是竹节一基纱的转换，都是一个平缓的渐变过程，转杯纺所获得的竹节呈两头细、中间粗、粗细平缓变化的长竹节。

表1为计算说明基纱一竹节转换阶段成纱增粗的渐变情况。

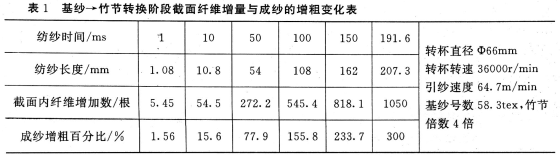
2基纱与竹节相互转换阶段成纱粗度变化规律

以上是从转杯纺成纱原理分析了成纱的粗度变化情况，下面进一步深入探讨这种变化规律。

2.1不考虑伺服电机升降速过程，转换阶段竹节粗度变化规律

不考虑伺服电机升降速过程，即认为伺服电机瞬间完成高低速给棉速度切换，且不考虑任何机械间隙停顿和滞后等因素。同时假设棉条经分梳辊充分分梳，完全及时剥离转移，以单纤维束进入转杯均匀铺设；转杯凝聚槽内纤维层呈直角楔形堆积分布，且楔形几何形态与纤维堆积量成正比，即与成纱线密度(号数)成正比。

图1为基纱一竹节转换过程中纤维层楔形变化情况。△OANBN为基纱一竹节开始时纤维层楔形状态，△OiAsiBi和△OsAsBs分别为任意时刻和基纱一竹节转换结束时，转杯凝聚槽内纤维层楔形形态。

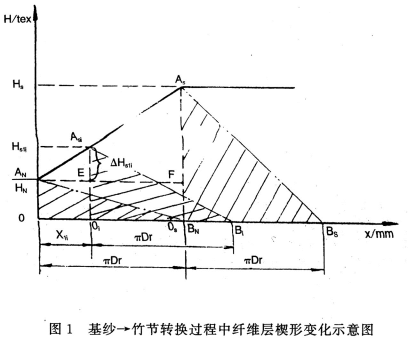
由图形几何关系不难得出任意引纱长度xli时的竹节粗度Hsli为：

即在基纱一竹节渐变过程中，竹节粗度是原基纱粗度与增量粗度之和。增量粗度△Hsli随着引纱长度Xli的增加而增大，当Xli=πDr，即一个转杯周长时，竹节粗度Hsli达最大值Hs，即基纱一竹节转换结束，进入竹节粗度值纺纱。而增量粗度△Hsli正比于(Hs—HN)，表明竹节与基纱的倍数越大，增量粗度增加越快。

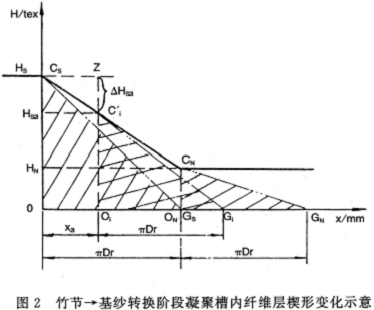
同理，从图2竹节一基纱转换阶段凝聚槽内纤维层楔形变化，

也不难得出任意引纱长度x2i时成纱粗度Hs2i为：

式中：△Hs2i——竹节→基纱任意时刻减量粗度号数(tex)；

x2i——竹节一基纱任意时刻引纱长度(mm)。

2.2考虑伺服电机升降速过程，转换阶段竹节变化规律

以上是假设基纱竹节转换过程中，伺服电机速度瞬间完成切换的情况，实际上不管这种切换速度有多快，总有一段加速或减速的过程，而这种短暂的升降速变化对转杯竹节纱形态变化有一定的影响。现先讨论基纱一竹节伺服电机加速过程中竹节粗度的变化情况。

假设伺服电机以等加速升速(其余上述假设不变)，那么就有以下关系式：

伺服电机转速升速倍数，即竹节精度倍数K为：

那么，伺服电机加速过程中，转杯凝聚槽内每层纤维的增量数△m为：

式中：——每层平均纤维根数(根/层)；

故伺服电机加速过程中转杯凝聚槽内单位时间内的增量纤维数△Mt为：

式中：b——单位时间内铺设的纤维层数(层/ms)；

于是在伺服电机加速过程中，任意时刻成纱截面内的累计增量纤维数△Msi为：

由上式可得伺服电机加速过程中任意时刻成纱所获得的增量粗度△Hsli为：

而伺服电机加速时间t与引纱长度xli有如下关系：

式中：Xli——伺服加速期任意时刻引纱长度(mm)。

所以用(13)式代入(12)式，可得用引纱长度表述的伺服加速期内增量粗度△Hsli为：

式(12)和(14)表明，伺服电机加速过程中，竹节粗度增量是加速时间

t或引纱长度x1i的两次函数。

由此可得伺服电机加速升速过程中，成纱的竹节粗度Hsli为原基纱粗度HN和增量粗度△Hs1i之和(参见图3)：

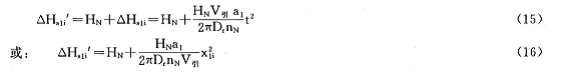
伺服电机在加速升速结束后即进入纺竹节状态，此时转杯凝聚槽内纤维增量速率与不考虑伺服电机升降速度时相同，所以在图3中可以从加速升速结束点作ANAS的平行线IA′s，就可求得基纱→竹节转换结束点A′s的位置。由图3可见，由于伺服电机升速加速过程的影响，基纱→竹节的转换长度有所延长，其延迟长度△A和基纱一竹节转换长度x1由以下公式求得。

式中：1I——伺服升速加速期引纱长度(mm)；

HsT——伺服升速加速期结束时竹节粗度(tex)。

同理，假如伺服电机在竹节一基纱转换初期是以等减速加速度完成速度切换，那么：

式中：a2——伺服电机减速加速度(r/ms2)；

t——减速降速时间(ms)。

用相同方法可得出竹节一基纱伺服电机降速过程中,任意时刻成纱粗度Hs2i′的计算公式为：

由公式(20)、(21)可知，在整个伺服降速期内竹节粗度呈两次函数递减变化。从D点起伺服电机降速完成进入纺基纱低速给棉。正如以上成纱原理分析所述，由于此时转杯凝聚槽内还残留着降速期结束时的HsD高量纤维层，要实现基纱粗度纺纱，必须待它们完全被剥离，即再经过一个转杯周长的引纱才能彻底完成这种切换。所以，实际竹节一基纱转换结束点延迟到C′N，而非不计伺服降速过程时的CN点。这两点间的引纱长度即为伺服降速延迟长度AC，其值为：

所以，竹节→基纱的实际转换长度x2为：

<

由图3关系还可得出竹节长度、基纱长度和一只竹节循环长度之计算公式：

公式(25)、(26)、(27)表明，实际竹节长度是竹节设置长度、转杯周长和伺服降速延迟长度之和；(紧接着的下一只)基纱长度为该基纱设置长度与转杯周长和上一只竹节伺服降速延迟长度之差；一只完整的竹节循环长度是竹节长度和(紧接着的)基纱长度之和。由上述分析可知，伺服电机的升速过程不影响竹节的总长度，但它缩短了竹节粗度值纺纱长度(当xs>x1)时，并使得基纱→竹节转换初期的竹节粗度增加变得更为平缓。伺服电机的降速过程会增加竹节的总长度和缩短下一只基纱纺纱长度，并使得竹节一基纱转换初期竹节粗度下降趋缓，这在一定程度上补偿了因伺服升速延迟使竹节粗度值纺纱长度的缩短。

以上是伺服电机在等加减升降速情况下的结论。在实际工作中，伺服电机的升降速过程并非全程恒等加减速变化，为了减少伺服过冲，在加速过程的末端速度变化有所趋缓，使竹节变化更为平缓，但不影响上述推论。

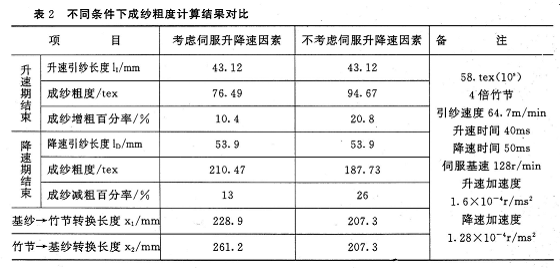
表2是根据以上推导公式，对纺58.3tex(10s)4倍竹节纱，引纱速度64.7m/min，伺服升速时间40ms，降速时间50ms时，计算得出的伺服升降速结束时成纱粗度与不考虑伺服升降速因素成纱粗度的对比结果。由表2可见，因伺服升降速因素的存在，基纱与竹节转换初期成纱粗度变化更为平缓，其基纱与竹节转换长度都有所延长。

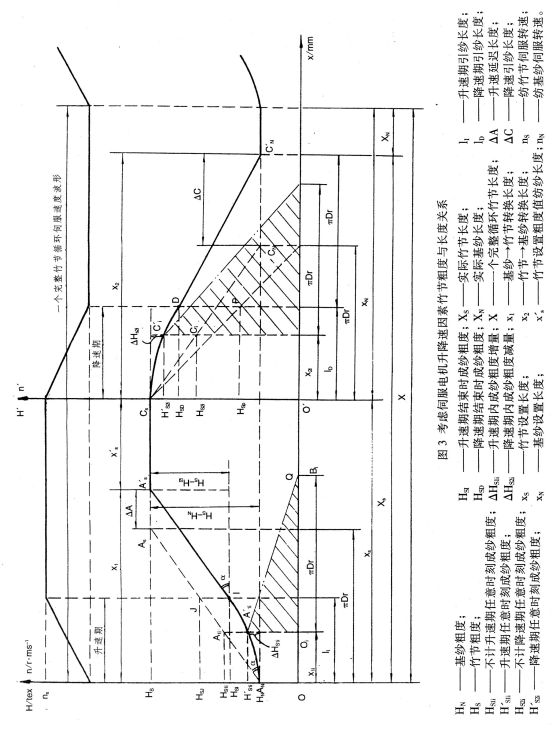
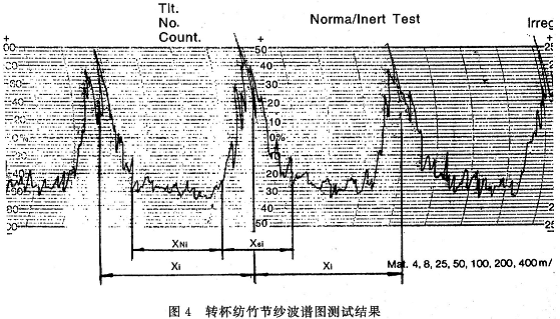
表3为上述纺纱品种与条件下，基纱设置长度840mm，竹节设置长度210mm一只竹节循环竹节纱，用乌斯特曲线图测量法(见图4)所测得的实际基纱长度XNi和循环长度Xi值。

由实测结果计算的竹节平均长度为：

而由公式(25)计算的竹节理论长度Xs为：

Xs=xs+πDr+1D=210+π×66+53.9=471.

2(mm)

由此可见，实际竹节长度与理论推导极为接近，其绝对误差为2.3mm，相对误差O.5％，说明上述推论是正确的。

3竹节参数设置与竹节长度、粗度和形态的关系

上述有关竹节长度、基纱长度计算公式可作为竹节参数设置的依据，但是它们之问的不同组合将会产生不同粗度和形态的竹节，以下分三种情况予以讨论。为讨论方便，不考虑伺服升降速过程，并假定竹节设置粗度不变。

3.1竹节设置长度大于等于转杯周长(xs≥πDr)，基纱设置长度大于等于转杯周长(XN≥πDz）

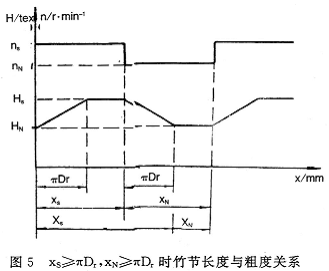
这是一种最为常见的设置方案，从图5关系中不难得出实际竹节长度和基纱长度值为：

Xs=xs+πDr (28)

XN=XN-πDr (29)

在这种设置情况下，竹节最大粗度与设置值相同，即均为Hs。

3.2竹节设置长度小于转杯周长(xs<πDr)，基纱设置长度大于等于转杯周长(xN≥πDr)

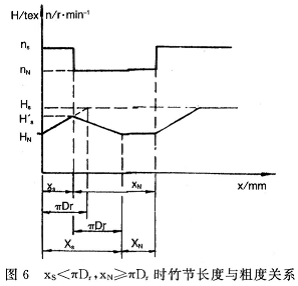
由图6可知，竹节长度和基纱长度同第1种情况，即：

Xs=xs+πDr

XN=XN-πDr

但是实际最大竹节粗度Hs′小于设置值Hs，其值为：

之所以最大竹节粗度小于设置值，是因为竹节设置长度小于基纱一竹节转换最短长度(一个转杯周长长度)。当竹节增粗尚未达设置值时，伺服即转为纺基纱低速给棉，于是竹节由增粗转为变细，从而无法达到设置值。但基纱粗度因其长度设置满足转换长度条件，故能得以保证。这种长度

设置组合，纺出的竹节粗细长度为不对称形，竹节设置长度越短这种不对称性越大。如果竹节长度设置尽量短(xs→零)，而竹节粗度设置得足够大(能产生明显竹节)的话，在理论上可获得的最短竹节长度为一个转杯周长长度。但是由于伺服升速特性和伺服传动系统承受极短暂高速变速惯性冲击能力的限制以及伺服降速延迟长度的影响。实际转杯纺所获得的最短竹节长度要大于转杯周长。

运用公式(30)也可反过来求得为获得较短竹节长度，采用小于转杯周长竹节长度设置时的竹节粗度计算公式：

式中：Hso——小于转杯周长短竹节长度设置时，竹节粗度设计号数(tex)。

Hs′——实际所需竹节粗度号数(tex)。

此式对于BD200系列纺纱器采用大中转杯纺制粗度不大的较短竹节有实际意义。

3.3竹节设置长度大于等于转杯周长(xs≥πDr)，基纱设置长度小于转杯周长(xN<πDr)

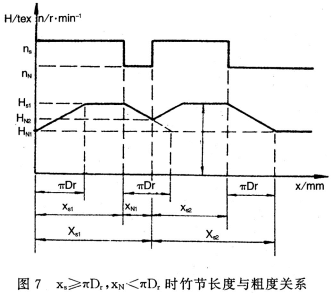
图7显示了连续两只竹节长度与粗度变化关系。由于第一只竹节基纱长度小于竹节一基纱转换长度，致使第一只竹节还来不及恢复到纺基纱状态，伺服又开始转为纺第二只竹节，故呈现双竹节状。其长度和粗度有如下关系式:

由于转杯纱竹节很长，这种双竹节将使竹节更长。

4结论

(1)由于伺服电机升降速过程的存在，使竹节与基纱的转换过程有所延长。实际竹节长度为竹节设置长度、转杯周长和伺服降速延迟长度之和；实际竹节粗度与竹节设置长度有关。

(2)采用小于转杯周长(实际应为基纱→竹节的转换长度)竹节长度设置时，能获得相对较短的竹节，但实际纺纱粗度小于设置值。小于转杯周长长度越长，竹节粗度与设置值差异越大。

(3)不同的竹节长度和基纱长度设置组合，会产生不同粗度和形态

的竹节。

参考文献

[1]上海纺织工学院棉纺教研室主编.棉纺学(下册).北京：纺织工业出版社，1981：439～446.

[2]沈天培译.气流纺纱工艺过程.北京：纺织工业出版社，1990；52～58.