转杯纺自由纱段曲线形状对剥离点附近捻度水平的影响

巴塔黄秀宝

(东华大学纺织学院)

摘要：通过对自由纱段的运动及受力分析，对自由纱段形态以及纺纱工艺参数对自由纱段捻度分布的影响进行了研究。研究表明：因自由纱段在杯内成弯曲形状，从而使得自由纱段捻度自假捻盘入口处向剥离点处不断减少，直至剥离点处纱条捻度甚至降到只有机械捻度的40%～80%。为了保证凝聚槽内一定的捻度传递长度，则需适当提高机械捻度，这就揭示了转杯纱机械捻度高于环锭纱的最根本原因。高速细号时的剥离点纱条捻度相对于低速粗号而言要高，说明只要一些纺纱工艺参数如纺杯直径、纺杯速度、假捻盘规格等配合得当，转杯纺也可高速稳定地纺制细号纱。

关键词：转杯纺纱；自由纱段；弯曲；捻度分布；捻度传递

0引言

转杯纱机械捻度为什么比相应的环锭纱高?自由纱段和剥离点附近纱条上到底有多少捻度?转杯纺杯内纱条的捻度究竟是如何分布的?过去研究工作[1-3]认为：引纱孔内一段纱条上是机械捻度，假捻盘上一段纱条中是机械捻度加上逐渐增加的假捻捻度，自由纱段上是机械捻度和假捻盘所施加最大假捻捻度之和，且一直保持到剥离点附近纱条上。既然剥离点纱条捻度是杯内纱条最高捻度(机械捻度+假捻捻度)，即使在向凝聚槽内须条传递捻度过程中会受凝聚槽壁的部分阻力矩，但转杯纱机械捻度和环锭纱机械捻度不应相差很多。

尽管有研究工作者[2]计算过自由纱段上的捻度分布，但未将自由纱段的弯曲[4-5]对捻度分布的影响考虑在内，因此认为杯内自由纱段的捻度分布是均匀的。根据有关文献资料[6-9]以及Singh[10]所拍的自由纱段图片看(见图1)，自由纱段曲线形状对加捻区域纱条的捻度分布是有影响的。由图1可以看出，剥离点附近自由纱段(图1中PB段)和假捻盘附近自由纱段(图1中BP1段)捻度相差比较大，这说明自由

纱段上的捻度并非均匀分布，而是一段捻度高、一段捻度低。因此，有必要对自由纱段曲线形状对其捻度分布以及剥离点附近捻度水平的影响进行研究。

1自由纱段受力分析

转杯纺纱正常纺纱时，杯内自由纱段以角速度ω绕转杯轴心线高速回转。假定转杯角速度为ωr，凝聚槽半径为R，引纱速度为v，则正向剥取时自由纱段绕转杯轴心线回转角速度应为：

ω=ωr+v/R

由于v/R相对于ωr比较小，为便于理论分析，取ω≈ωr。

如图2(a)所示，取剥离点P及假捻盘入口P1点之间的自由纱段为研究对象。其中，r1为假捻盘外半径，T1和TR分别表示自由纱段两端张力，转杯轴心线垂直于纸面通过01点。如图2(d)所示，在该自由纱段上取含O点的微元纱段ds，并建立直角坐标系O-xyz，其中Oxyr为微元纱段ds所在的平面，x轴沿着微元纱段ds的切线方向，y轴沿着微元纱段ds的主法线方向，z轴沿着微元纱段ds的副法线方向。另外，以极坐标(θ，r)作为自由纱段的曲线轨迹坐标，θ为纱条在转杯内任意点处的极角，r为自由纱段上任意点的极径，如图2(b)所示。在图2(c)中，入为自由纱段任意点切线与转杯径向之间的夹角，dβ为微元纱段ds对曲率中心的包角，q为转杯轴心线到自由纱段曲线上任意点切线的垂距。

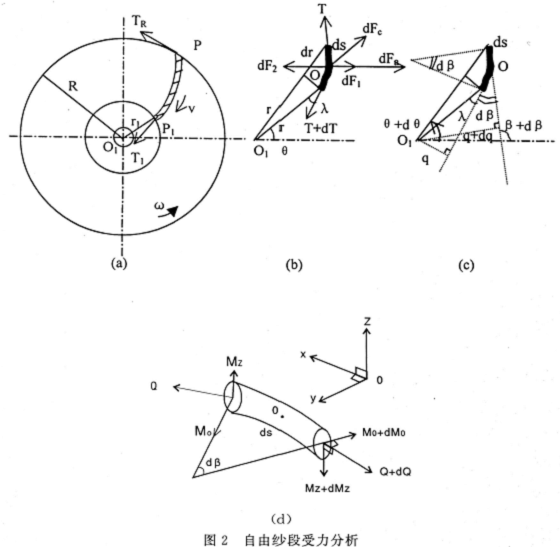
微元纱段ds上所受的力有：两端作用有张力T和T+dT，沿着微元纱段ds两端的切线方向；微元纱段随纱条绕转杯轴心线回转而产生的牵连运动惯性力为dFc=mrω2ds，方向沿着转杯径向，式中m为纱条线密度；空气阻力dFa=cdρry(rωcosλ)2ds[11]，方向沿着微元纱段主法线，式中cd为空气阻力系数，ρ为空气密度，ry为纱条半

径；纱条引纱运动引起的相对运动惯性力dF1=mv2dβ、哥氏惯性力dF2=2mvωds.方向均沿着微元纱段主法线。上述各力方向见图2(b)。由于纱线弯曲而产生的弯曲剪力、微无纱段ds所受重力以及切向空气阻力均比较小，可略去不计。因加捻而产生的微元纱段ds两端扭矩为Q、Q+dQ，其矢量方向沿着使微元纱段两端切线；由于微元纱段ds在Oxz平面上弯曲而产生的弯曲力矩Mz，其方向沿着z轴；由于微元纱段ds两端扭矩Q、Q+dQ的作用而使微元纱段ds在Oxz平面上也产生弯曲的趋势，但不发生实际弯曲，其原因下面将有解释。根据有关文献资料[9，12]，纱条有弯曲的趋势而无实际弯曲发生时，其抗弯力矩主要产生于纤维之间的摩擦以及张力等因素，其大小可表示为[12]；

Mo=(1一f)(μfty/πtf)Trysinδcosδ(6一COS2δ)/6

式中：f为一系数，用来修正纱线离开纺纱过程后的松弛对Mo的影响(由于本文所研究的纱条处于纺纱过程中，因此可取f—O)，δ为纱线表面螺旋角，μf为纤维间摩擦因数，T为纱线所受张力，ry为纱线半径，ty为纱线特数，tr为纤维特数；Mo矢量与Q的矢量均在Oxy平面内，且相互垂直，如图2(d)所示。

根据图2(b)中力的平衡，微元纱段ds上作用的力在x、y轴上投影，得：

根据图2(d)中力矩的平衡，力矩在x、y、z轴上投影并略去高阶项得：

从式(4)可看出，加捻扭矩在y轴上的分量Qdβ会促使纱条在Oxz轴上产生弯曲的趋势，之所以没有产生实际弯曲，是因为Odβ的大小还不至于克服纱线有弯曲趋势时所产生的、纱线中纤维相互间摩擦以及张力等引起的dMo。此外，作用在Oxy平面上的张力也会维持微元纱段只在其

平衡平面内的弯曲，因为即使是当Qdβ大到克服dMo，使纱条在Oxz轴平面上产生实际弯曲时，由于该平面上没有其他的力可平衡于张力，因而也无法保持其在Oxz平面上的弯曲形状。

通过式(3)可看出，杯内自由纱段的加捻力矩增量dQ主要用来克服自由纱段处于平面弯曲状态时的抗弯力矩Modβ。

由图2(c)几何关系有：

式中：Nf为纱线截面纤维根数：KfGt为纤维抗扭刚度。

由于目前还没有适合于转杯纱加捻扭矩Q和弯曲趋势力矩Mo的计算公式，需对上述计算式中的Nf进行修正。考虑到转杯纱是由纱芯和包缠纤维组成的两相特殊结构，并注意到Nfr=cfNf=cfty/tf，式中Nft为转杯纱截面中纱芯部分的纤维根数；cf为一修正系数，可由下式表示[15]：

其中：s为捻度传递长度；L为纤维长度；c为纤维长度变异系数。

Q和Mo可改写为：

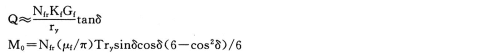
Q式两端对q取微分，得：

代入式(8)，得：

再由q的定义及图2(b)中的几何关系，有：

上式两端除以dp得：

这样，式(6)、(11)及(7)、(10)构成了自由纱段的形态及力学微分方程组，可通过数值法(本文使用四阶龙格库塔法)求解。其边界条件为：

假捻盘入口处：θ=O，q1，tanδ1，T1可由文献[2]求得；

剥离点处：q—R。

2自由纱段捻度分布计算结果及讨论

上述分析表明，转杯纺纱加捻点处产生的真捻捻度和假捻盘上产生的假捻捻度在自由纱段上的传递过程中，因自由纱段存在的弯曲会减少一部分加捻扭矩，用于克服纱线的抗弯力矩Mo，使得自由纱段捻度呈“捻陷性”分布。假定成纱捻度为two，杯内任意点纱条捻度为tw，则可用tw/two。来表示自由纱段上的

捻度变化的情况。为了对整个杯内纱条的捻度变化情况有所了解，对假捻盘上纱条的捻度分布也用tw/two来表示，这部分可参考文献[2]进行计算。计算所用原料参数为：棉纤维长度28.17mm，细度0.18tex，纤维抗扭刚度1.1×10-5cN·cm2，纤维间摩擦因数μf=O.29。

有关生产工艺参数见表1。

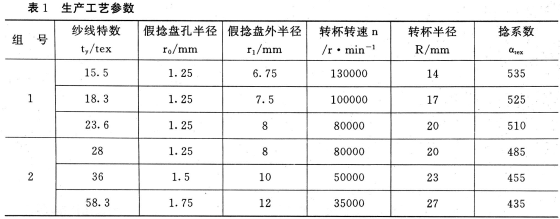
纱条与假捻盘的动摩擦因数由WIRA[16]资料进行曲线拟合得：

μ=O.2041666—0.325×10-4×V∑+0.5833333×10-7×V∑

这里，使用了生产中较为常用的高速细号和低速粗号两组工艺作为计算参数，计算结果如图3所示，图中：O1M段为引纱孔内纱段捻度分布，MP1为假捻盘上纱段捻度分布，P1P为自由纱条上捻度分布，P为剥离点处捻度。

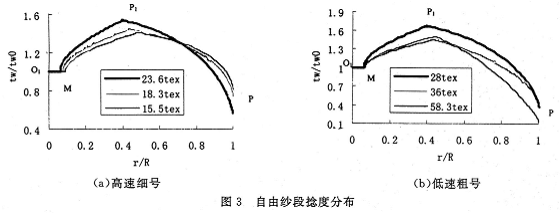
由图3可以看出：假捻盘假捻作用使杯内纱条捻度增大(图中MP1)，而自由纱段的弯曲则使加捻点处产生的真捻和假捻盘上产生的假捻捻度在传递过程中减少(图中P1P段)，这部分减少的捻度就是用来克服纱线抗弯力矩M0的；自由纱段上捻度在剥离点(r/R=1)附近呈加速减少趋势，甚至减少到只有机械捻度的40%～80%不等，这是由于剥离点附近自由纱段曲率较大，导致需要更大的加捻扭矩克服纱线抗弯力矩Mo，这可能就是转杯纱机械捻度要比相应的环锭纱要高的最根本原因；另外，剥离点处(r/R=1)捻度大小随纺纱工艺的不同而变化，这是因为传递到剥离点处的捻度取决于自由纱段曲线形状以及纱线的抗弯力矩Mo的大小，而纱线曲线形状和Mo则取决于纺纱工艺以及纤维性能；高速细号组剥离点处捻度相对于低速粗号组而言要高，这主要是在高速细号条件下，虽速度提高会使纱线离心力增大，但纺杯尺寸减小、纱号变细又会使

离心力降低，从而有可能使T变化不大，但纱变细，ry变小，从而使Mo变小所致，这说明高速细号纱的纺纱稳定性比低速粗号纱要好一些。

3结论

通过上述分析、推导以及计算，可得到以下结论：

(1)转杯纺纱杯内自由纱段的曲线形状对其捻度分布有很大影响。自由纱段上捻度自假捻盘人口端向剥离点端呈逐渐减少趋势，在靠近剥离点附近时，这种趋势加快。

(2)纺纱工艺参数对剥离点处纱条的捻度有影响。高速细号时的剥离点纱条捻度相对于低速粗号而言要高，这说明只要一些纺纱工艺参数如纺杯直径、纺杯速度、假捻盘规格等配合得当，高速细号纺纱稳定性未必差于低速粗号时的纺纱稳定性。

(3)转杯纱捻度一般高于相应环锭纱，自由纱段的形态弯曲是主要原因。

参考文献

[1]张百祥，周慈念等.阻捻盘假捻作用的分析.上海棉纺学术年会论文集，1983，616～623.

[2]汪军，黄秀宝.转杯纺杯内纱段捻度分布研究.中纺大学报.1999；(6)：51～54.

[3]P.R.Lord.TheTwiststructureofOpen—EndYarns.T.R.J，1976；(2)：123～129.

[4]ChenRenzhe.OntheYarnDynamicsintheoESpinningRotors.J.c.T.u，Jan，1986.

[5]Ripka.YarnMechanicsintheSpinningRotor，Collection0fPapersonOEspinning，prague，1967.

[6]J.J.Thwaits.YarnBendingintheFalseTwistProcess，J.T.I，1987；(3)：152～163.

[7]J.J.Thwaites.TensionandTorqueGenerationin

theDiskSpindle.J.T.I，1985；76：157～170.

[8]F.Goktepeeta1.DeformationofaSingleHelixunderSimultaneousApplicationofExtension.Compression，andBending.T.R.J，2000；70(6).508～518.

[9]Lear，G.A.V.TheBendingBehaviorofaHelicalFilament，Part2：Curvture，TwistandStrainEnergy.J.T.I，1979；70：330～336.

[10]VijaiPalSingh.TheTwistCharacteristicsinOpen—endSpunYarns，DoctorialThesis.theU—niversityofleeds.1980；12.

[11]张文赓等.纺织气流问题.北京：纺织工业出版社，1989：266.

[12]G.A.V.Leaf.TheFrictionCoupleinYarnBending.J.T.I，1995；86(1)：45～54.

[13]PostleReta1.TheTorqueinTwistedSinglesYarn.J.T.I，1964；55(9)：448461.

[14]PlattMeta1.TorqueDevelopmentinYarnsSystem：SingleYarn.T.R.J，1958；28(1)：1～14.

[15]theGeometryandStrengthofYarnsWithSpecialReferencetoRotorSpunYarns，P.GrOsbergandK.H.Ho，AppliedPolymerSymposia，1997；3

1：83~89.

[16]AlexRae，RolloBruce.theWIRATextileDataBook，Britain，1973；B116.